پاوپوینت آماده کاربرد نقاط کوانتومی در شیمی تجزیه به زبان انگلیسی

اختصاصی از سورنا فایل پاوپوینت آماده کاربرد نقاط کوانتومی در شیمی تجزیه به زبان انگلیسی دانلود با لینک مستقیم و پر سرعت .

این محصول شامل 34 اسلاید مفید و کاربردی در مورد کاربرد نقاط کوانتومی در شیمی تجزیه اعم از اسپکتروسکوپی و الکتروشیمی می باشد.

تحقیق درباره ی کوانتومی 107 ص

اختصاصی از سورنا فایل تحقیق درباره ی کوانتومی 107 ص دانلود با لینک مستقیم و پر سرعت .

لینک دانلود و خرید پایین توضیحات

فرمت فایل word  و قابل ویرایش و پرینت

تعداد صفحات: 109

فهرست مطالب

پیشگفتار 1

1- درهم تنیدگی و جداپذیری 4

1-1 –حالت 5

1-2- فضای هیلبرت 5

1-3- کیوبیت 5

1-4- ماتریس چگالی 6

1-4-1- عملگر چگالی تقلیل یافته 6

1-4-2- ترانهاده جزئی 7

1-5- درهم تنیدگی و جداپذیری 7

2- ملاکهای تشخیص درهم تنیدگی 10

2-1- معیارهای عملیاتی 11

2-1-1- معیار پرس 11

2-1-2- معیار تقلیل یافتگی 13

2-1-3- معیار تفوق 15

2-1-4- معیار هم ترازی 17

2-2- معیارهای غیر عملیاتی 20

2-2-1- معیار نگاشت مثبت 20

2-2-2- معیار گواه های در هم تنیدگی 21

3- مقیاسهای در هم تنیدگی 22

3-1- آنتروپی فون نیومن 23

3-2- مقیاس درهم تنیدگی قابل تقطیرومقیاس هزینه درهم تنیدگی 23

3-3 –درهم تنیدگی ساختار 24

3-3-1- یک زوج کیوبیت 25

3-3-2- حالت ورنر 26

3-4- منفیت 27

3-5- روش تجزیه 28

3-6- درجه درهم تنیدگی برای یک سیستم کیوبیت کیوتریت در حالت خالص ....29

4- پیدا کردن حالتهای با بیشترین درهم تنیدگی برای سیستم کیوبیت –کیوتریت 33 4-1- محاسبه ضرایب اشمیت برای سیستم کیوبیت–کیوتریت 34

4-2- محاسبه حالتهای با حداکثر درهم تنیدگی برای سیستم کیوبیت–کیوتریت 35

4-3 – مقایسه با چند مقیاس درهم تنیدگی 37

4-3-1 آنتروپی فون نیومن 37

4-3-2- درهم تنیدگی ساختار 38

4-3-3- منفیت 38

5- ارتباط از راه دور 40

5-1- مفهوم ارتباط از راه دور 41

5-2- ارتباط از راه دوراستاندارد 41

5-3- ارتباط از راه دورهمراه با نوفه 44

5-3-1- عوامل تولید نوفه 44

5-3-1-1- کانال معیوب 44

5-3-1-2- عملگرهای معیوب 45

5-3-1-3- اندازه گیری معیوب 45

5-3-2- اعمال عوامل نوفه در فرایند ارتباط از راه دور 46

6- درهم تنیدگی کمکی49

6-1- درهم تنیدگی کمکی 50

6-2- ماکزیمم احتمال تقطیر یک حالت بل از حالت سه تایی اولیه 51

6-3- رده Ą 52

6-4- شرایط رده Ą 53

6-5- اندازه رده Ą 55

6-5-1- روش تحلیلی 55

6-5-2- روش عددی 57

6-5-2-1- سیستم 2×2×2 58

6-5-2-2- سیستم 4×2×2 59

پیوست 1 : جبر خطی 61

پیوست 2 : تجزیه اشمیت 66

پیوست 3 : عملیات موضعی وارتباطات کلاسیکی LOCC 67

مراجع 68

واژه نامه 73

پیشگفتار :

حدود70 سال پیش، اروین شرودینگر نام Verschrankung را به طبیعت همبستگی کوانتومی اطلاق کرد ] Sch35 .[ درز بان محاوره آلمانی برای مردم غیرفیزیکدان این اصطلاح به معنای " مچ انداختن " کار می رود. این واژه درزبان انگلیسی Entanglement و درزبان فارسی در هم تنیدگی ترجمه شده است که درمعنای ضمنی خود رساتر می باشد . در هم تنیدگی کوانتومی ، نخستین بار در سال 1935 ، توسط انیشتن و همکارانش پادولسکی و روزن1 ، ] EPR35 [ به طور جدی مورد بحث قرار گرفت . ایده این دانشمندان به صورت پارادوکسی با حروف اول اسامی آنها یعنی EPR

پاورپوینت کامل و جامع با عنوان درس مبانی شیمی کوانتومی در 219 اسلاید

اختصاصی از سورنا فایل پاورپوینت کامل و جامع با عنوان درس مبانی شیمی کوانتومی در 219 اسلاید دانلود با لینک مستقیم و پر سرعت .

دید کلی

شیمی کوانتومی ، دانش کاربرد مکانیک کوانتومی در مسایل مربوط به شیمی است. اثر شیمی کوانتومی ، در شاخه‌های وابسته به شیمی قابل لمس است. مثلا :

• علمای شیمی فیزیک ، مکانیک کوانتومی را (به کمک مکانیک آماری) در محاسبات مربوط به خواص ترمودینامیکی (مانند آنتروپی و ظرفیت حرارتی) گازها ، در تفسیر طیفهای مولکولی به منظور تائید تجربه خواص مولکولی (مانند طولها و زوایای پیوندی) ، در محاسبات نظری خواص مولکولی ، برای محاسبه خواص حالات گذار واکنشهای شیمیایی به منظور برآورد ثابتهای سرعت واکنش ، برای فهم نیروهای بین مولکولی و بالاخره برای بررسی ماهیت پیوند در جامدات بکار می‌برند.
  
  
• علمای شیمی آلی از مکانیک کوانتومی ،‌ برای برآورد پایداریهای نسبی مولکولها ، محاسبه خواص واسطه‌های واکنش ، بررسی ساز و کار واکنشهای شیمیایی ، پیش بینی میزان ترکیبات و تحلیل طیفهای NMR استفاده می‌کنند.
  
  
• علمای شیمی تجزیه از مکانیک کوانتومی برای تفسیر شدت و فرکانسهای خطوط طیفی استفاده می‌کنند.
  
  
• علمای شیمی معدنی از نظریه میدان لیگاند که یک روش تقریبی مکانیک کوانتومی است، در توضیح خواص یونهای مرکب فلزات واسطه سود می‌برند.

فرضیه پلانک ، سرآغاز مکانیک کوانتومی

در سال 1900، "ماکس پلانک" ، نظریه‌ای ابداع کرد که با منحنی‌های تجربی تابش جسم سیاه ، مطابقتی عالی از خود ارائه داد. فرض او این بود که اتمهای جسم سیاه ( ماده‌ای که تمام نورهای تابیده به آن را جذب کند ) ، تنها قادرند نورهایی را گسیل سازند که مقادیر انرژی آنها توسط رابطه hv داده می‌شود. در رابطه ، v فرکانس تابش و h ، ثابت تناسب است که به ثابت پلانک معروف است. با قبول مقدار 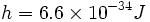، منحنی‌هایی بدست می‌آیند که با منحنی‌های تجربی جسم سیاه کاملا مطابقت دارند. کار پلانک سرآغاز مکانیک کوانتومی بود.

به دنبال پلانک ، "انیشتین" نیز مشاهدات مزبور را بر اساس اندیشه تشکیل نور از اجزایی ذره گونه تشریح کرد که آنها را فوتون نامید که انرژی هر یک از آنها برابر است با: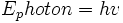

احتمال و مکانیک کوانتومی

موضوع احتمال ، یک نقش اساسی را در مکانیک کوانتومی ایفا می‌کند. در مکانیک کوانتومی ، سروکار ما با احتمالاتی است که با متغیر پیوسته‌ای مانند مختصه x درگیرند. صحبت از احتمال پیدا شدن یک ذره در یک نقطه خاص مانند x = 0.5000 حاوی چندان معنایی نیست، زیرا تعداد نقطه‌ها در روی محور xنامتناهی ، ولی تعداد در اندازه گیریهای ما به هر حال متناهی است و از این رو ، احتمال وصول با دقت به 0.5000 بی‌نهایت کم خواهد بود.

این است که به جای آن از احتمال یافتن ذره در یک فاصله کوتاه از محور x ، واقع بین x+dx , x صحبت می‌شود که در آن dx یک طول بینهایت کوچک است. طبیعتا احتمال فوق متناسب با فاصله کوچک dx بوده و و برای نواحی مختلف محور x متغیر خواهد بود. بنابراین احتمال اینکه ذره در فاصله مابین x و x+dx پیدا شود، مساوی g(x)dx است که در اینجا (g(x بیانگر نحوه تغییرات احتمال روی محور x است. تابع (g(x چون برابر مقدار احتمال در واحد طول است، لذا چگالی احتمال نامیده می‌شود.

چون احتمالات ، اعداد حقیقی و غیر منفی‌اند، لذا (g(x باید یک تابع حقیقی باشد که همه جا غیر منفی است. تابع موج 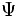می‌تواند هر مقدار منفی و یا مقادیر مختلط را به خود بگیرد و از این نظر به عنوان یک چگالی احتمال محسوب نمی‌شود. مکانیک کوانتومی به عنوان یک اصل می‌پذیرد که چگالی احتمال برابر است.

اصل عدم قطعیت هایزنبرگ

اندیشه "بوهر" مبنی بر اینکه هر الکترون در اتم ، تنها می‌تواند کمیتهای معین انرژی را دارا باشد، گام مهمی در رشد و تکوین نظریه اتمی بود (مدل اتمی بوهر). نظریه بوهر برای توجیه طیف اتم هیدروژن ، مدلی رضایت بخش ارائه کرد، اما تلاش برای بسط نظریه به منظور تشریح طیف اتمهای دارای بیش از یک الکترون ناموفق بود. دلیل این مشکل به زودی آشکار شد.

در نگرش بوهر ، الکترون به عنوان ذره‌ای باردار متحرک ، در نظر گرفته می‌شود. برای پیش بینی دقیق مسیر یک جسم متحرک ، دانستن مکان و سرعت جسم در هر لحظه معین ضروری است. اصل عدم قطعیت هایزنبرگ (19266) نشان می‌دهد که تعیین دقیق مکان و اندازه حرکت جسمی به کوچکی الکترون ناممکن است. هرچه تلاش کنیم که یکی از این کمیتها را دقیقتر تعیین کنیم، از دقت کمیت دیگر ، نامطمئن‌تر هستیم.

مشاهده اشیا با دریافت انعکاس پرتوهای نوری که برای روشن کردن آنها بکار رفته است، امکان‌پذیر است. برای تعیین موقعیت جسمی به کوچکی یک الکترون ، تابشی با طول موج به غایت کوتاه مورد نیاز است. چنین تابشی ،‌ طبعا فرکانس بسیار بالایی خواهد داشت و بسیار پرانرژی خواهد بود. وقتی این تابش به الکترون برخورد کند، سبب تغییر تندی و جهت حرکت آن می‌شود. از این رو هر گونه تلاش برای تعیین موقعیت الکترون ، اندازه حرکت آن را به شدت تغییر می‌دهد. فوتونهایی که طول موج بلندتر دارند، کم انرژی‌ترند و تاثیر کمتری بر اندازه حرکت الکترون می‌گذارند، ولی به علت بلندی طول موجشان ، نخواهند توانست موقعیت دقیق الکترون را نشان دهند.

از این رو ، این دو نوع عدم قطعیت با هم مرتبطند. به گفته هایزنبرگ ، حاصلضرب عدم قطعیت در مورد یک شیء ، 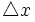و عدم قطعیت در اندازه حرکت آن ، ، برابر یا بزرگتر از حاصل بخش ثابت پلانک ، h و 4π است:

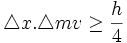
عدم قطعیت در اندازه گیری ، برای اشیایی به کوچکی الکترون بسیار مهم است، در حالی که برای اشیا با اندازه معمولی بی‌اهمیت است.

معادله شرودینگر

اصل عدم قطبیت هایزنبرگ نشان می‌دهد که هر نوع کوشش در راه جامعتر و دقیق کردن مدل بوهر ، بی‌نتیجه است، زیرا تعیین دقیق مسیر الکترون در یک اتم ناممکن است. از سوی دیگر ، "شرودینگر" ، رابطه دوبروی را برای تدوین معادله‌ای بکار برد که الکترون را برحسب خصلت موجی آن توصیف می‌کند.

معادله شرودینگر پایه مکانیک موجی است. معادله برحسب یک تابع موجی 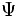برای الکترون نوشته می‌شود. وقتی معادله برای الکترون در اتم هیدروژن حل می‌شود، یک سلسله تابع موجی بدست می‌آید. هر تابع موجی به یک حالت معین انرژی برای الکترون مربوط است و ناحیه‌ای در اطراف هسته را توضیح می‌دهد که در آن ،‌ امکان یافتن الکترون وجود دارد. تابع موجی یک الکترون آنچه را که یک اوربیتال نامیده می‌شود، توضیح می‌دهد.

شدت هر موج ، با مجذور دامنه آن متناسب است. تابع موجی ، ، تابع دامنه است. مقدار برای یک حجم کوچک در هر موقعیتی در فضا ، متناسب با چگالی بار الکترونی در آن حجم است.

می‌توان تصور کرد که بار الکترون به سبب حرکت سریع الکترون به صورت ابر باردار در فضای دور هسته گسترده شده است. این ابر در برخی نواحی غلیظتر از نواحی دیگر است. احتمال یافتن الکترون در هر ناحیه معین متناسب با چگالی ابر الکترونی در آن ناحیه است. این احتمال در ناحیه‌ای که ابر الکترونی غلیظتر است، بیشتر خواهد بود. این تفسیر کوششی برای توصیف مسیر الکترون ، به عمل نمی‌آورند، بلکه فقط پیش بینی می‌کند که احتمال یافتن الکترون در کجا بیشتر است.

فهرست مطالب:

فصل اول: مکانیک کلاسیک منظومه های ذره ای

مختصات و درجه های آزادی منظومه

سرعت و تکانه ذره

معادله دیفرانسیل حرکت

تکانه زاویه ای

مولفه تکانه زاویه ای

کار انرژی جنبشی و انرژی پتانسیل

انرژی جنبشی

انرژی پتانسیل

اصل بقای انرژی

مکانیک لاگرانژ،هامیلتون و ژاکوبی

و...

فصل دوم: پایه های مکانیک کوانتومی

کاربرد مکانیک کوانتومی

آزمایش دو شکاف

رابطه دوبروی

اصل عدم قطعیت

و...

فصل سوم: اصول موضوع مکانیک کوانتومی

تابع موجی یا تابع حالت

اصل موضوع اول

شرایط مرزی و نرمالیزه بودن تابع موجی

شرط نرمالیزه

اصل موضوع دوم: اپراتورها

خواص اپراتورها

اپراتور خطی

اپراتور هرمیتیک

اپراتور انرژی پتانسیل

اپراتور انرژی جنبشی

اپراتور هامیلتونی

تابع ویژه و مقدار ویژه اپراتور

اصل موضوع سوم

اصل موضوع چهارم: معادله شرودینگر

معادله شرودینگر مستقل از زمان

و...

فصل چهارم: مطالعه چند الگوی کوانتومی ساده

ذره آزاد

ذره در جعبه یک بعدی

ذره در جعبه سه بعدی

نوسانگر هارمونیک

حل معادله دیفرانسیل هرمیت

توابع ویژه نوسانگر هارمونیک

حرکت ارتعاشی مولوکولها

چرخنده صلب

و...

فصل پنجم: حرکت در فضای سه بعدی

تکانه زاویه ای

اپراتورهای وابسته به تکانه زاویه ای

مفهوم فیزیکی جابجایی پذیری اپراتورها

و...

فصل ششم: اتم هیدروژن

نامگذاری حالتهای کوانتومی اتم تک الکترون

طرز نمایش و تعبیر فیزیکی اوربیتالهای اتمی

تابع توزیع شعاعی

سطوح تک دانسیته

اسپین

و...

تحقیق و بررسی در مورد فیزیک کوانتومی

اختصاصی از سورنا فایل تحقیق و بررسی در مورد فیزیک کوانتومی دانلود با لینک مستقیم و پر سرعت .

لینک دانلود و خرید پایین توضیحات

فرمت فایل word  و قابل ویرایش و پرینت

تعداد صفحات: 30

دنیای وارونه از محاسبات مقداری

ایده های عجیب و غریب می‌‌تواند منشأ کاملاًمعمولی داشته باشد.ایده کنونی زادگاهی به نام تگزاز دارد.در سال 1981 ویلر پدر روزنه سیاه و فیزیک نظری از دانشگاه تگزاز در آستین جلسه‌ای تشکیل داد.همه‌ی مهمان ها فیزیک‌دانهایی جوان با علاقه‌های مشترک دربنیان محاسبات بودند،همان موضوعی که ویلر به آن اعتقاد داشت،و در آن سال اهمیت افزونتری یافت .در این جلسه بود که بحث و مکالمه با چالز بنت ،یک فیزیک دان ABM ،جرقه‌ای را در ذهن یکی از محققان دانشگاه آکسفورد به نام دیوید دسچ ایجاد کرد.او بر این عقیده بود که نظریه محاسبات (کامپیوتر) بر روی قانونهای نیوتن بنا نهاده شده است،نه بر اساس توصیفات اساسی دنیا که بوسیله تئوری کوانتوم حمایت می‌شوند.

در هر صورت،صنعت کامپیوتر برای تحریک بیش از اندازه ریز تراشه‌ها شروع به کار کرده بود. این صنعت محاسبات بسیار گسترده‌ای را در هر ثانیه ممکن ساخته بود.اگر چه گرمای تولید شده باعث باقی ماندن ابدی سیلسیوم می‌شد ،برای رفع این مشکل دانشمندان تئوری مذکور رادر سال 1930 با پیشگامی ‍“آلان ترنینک” ارائه کردند .اما در جلسه ویلر ،داچ عقیده داشت “خیلی زودتر از حد انتظار ما خواهیم دید که با استفاده از قانونها ‹ماشین کوانتوم› ما به جوابهای متفاوتی خواهیم رسید.

داچ کار خود را ابتدا به صورت کتبی بر روی کاغذ شروع کرد که حالا ما نتایج آن را به صورت ملاحظاتی کلاسیک در این زمینه مشاهده می‌کنیم .این نتایج در سال 1985 منتشر شدند.نتایج نشان می دهد چطور کامپیوتر ها از قانون عجیب نیرو برد کوانتوم استفاده می‌کنند وچرا چنین کامپیوتر هایی اساساًبا کامپیوتر های معمولی تفاوت دارند.

15سال بعد انقلابی را که داچ شروع کرد به تناسبی جهانی رسید.چنین کامپیوتر هایی برای مدت طولانی به عنوان وسیله‌ای مرموز وجادویی باقی ماندند اما به صنعت آینده کامپیوتر قدرتی عجیب بخشیدند وبعد از آن بحث جابجایی و تغیر مکان آن‌ها پیش آمد مشروط به آنکه به آن حد انتظار می‌رسند یا نه؟هیجان انگیز بودن این مسئله به قدرتش وامدار ومقروض نخواهد بود.هر چند که بدون شک مدلهای امروزی این نمونه قدرت بسیار بالاتری دارند.

نقطه برتری چنین کامپیوتر هایی ،حل مسائل و انجام محاسباتی است که اساساً بوسیله کامپیوتر های قراردادی اصلاً قابل انجام نیستند.این همان پتانسیل و نیروی بالقوه‌ای است که باعث می‌شود برنامه تجارت کامپیوتر وبزرگترین برقراری ارتباطهای راه دور جهانی رونق فراوانی بیابد.این کمپانی ها شامل ABM ،هولت پاکارد ،لوسنت تکنولوژی ،AT،T،ماکروسافت.حتی پایگاهی در شهر نیویورک بنا شده است که «مجیک تکنولوژی » نامیده می‌شود.و امید وار است با مجهز شدن در این زمینه به پول زیادی برسد.به وسیله یکی از قدرتمندترین نیروهایی که از گسترش و توسعه کامپیوتر های کوانتوم ساطع شده است،آنها به راحتی کدهای سری تأثیر ناپذیر و غیر قابل نفوذ را خواهند شکست. آهنگ و زنگ خطر این مسئله در سال1994 به صدا در آمد

دانلود مقاله کامپیوترهای کوانتومی

اختصاصی از سورنا فایل دانلود مقاله کامپیوترهای کوانتومی دانلود با لینک مستقیم و پر سرعت .

عنوان مقاله :  کامپیوترهای کوانتومی

 قالب بندی :  Word

تعداد صفحات :40

شرح مختصر : اغلب کامپیوترهای دیجیتال امروزی برمبنای بیتها یا بایت هایی کار میکنند که محدود به0و1 هستند. کنند.اما رایانه کوانتومی وسیله‌ای محاسباتی است بجای بیتها دارای کیوبیت ها است.کوبیت مخفف کوانتوم-بیت است و از ویژگی حرکت چرخشی یا اسپینی الکترون ها در آن استفاده میشود که هر زمان نمایانگر بیش از یک عدد است. یک کامپیوتر مبتنی بر بیت های کوانتومی تعداد حالات پایه بیشتری نسبت به کامپیوترهایی بر پایه بیت های معمولی دارد، به طور همزمان می تواند دستورات بیشتری اجرا کند. یکی از قابلیت های کامپیوترهای کوانتومی که موجب تفاوت آنها با کامپیوترهای کلاسیک میشود بحث موازی بودن ذاتی پردازش درآنها است. درکامپیوترهای کوانتومی بزرگترین مشکل تشخیص وتصحیح خطا است. کامپیوترهای کوانتومی مبتنی بر فوتون ها کمترین اثر پذیری از محیط را دارند پس دارای احتمال خطای بسیار کمی هستند، کامپیوتر کوانتومی به عنوان یک ماشین محاسبه گر از گیت های منطقی برای پردازش اطلاعات بهره میبرد تفاوت عمده میان گیت های منطقی کلاسیک و کوانتومی آن است که ورودی وخروجی گیت های کوانتومی میتواند حالت برهم نهاده یک کیوبیت هم باشدیکی از گیت های منطقی کوانتومی،گیت CNOT است.  امروزه کامپیوترها به سرعت درحال نزدیک شدن به محدودیتی بنیادین هستند . شاید بزرگترین ضعف آن ها این است که متکی برفیزیک کلاسیک هستند که برازدحام پربرخورد میلیاردها الکترون درون تقریبا همان تعداد ترانزیستورحکم رانی می کنند .تراشه های درون کامپیوترهای امروزی به قدری کوچک می شوند که تداوم حکم رانی فیزیک کلاسیک ممکن نیست

فهرست :  

پیشگفتار وتاریخچه

کاربرد کامپیوترهای کوانتومی

نگاهی به محاسبات کوانتومی

منطق کوانتومی

پردازش کوانتومی

فیزیک محاسبات کوانتومی

تجزیه ناپذیری

برهم نهی

عملیات محاسباتی وentengliment

گیت ها

عملگرها

محدودیت های کامپیوترهای کوانتومی

به سوی کامپوترهای کوانتومی بر پایه تراشه

 پنج چیز که هر کامپیوتر کوانتومی نیاز دارد